3 min read

American option pricing is the binomial options pricing model that provides a generalizable numerical method for the valuation of options.
American options are contracts that may be exercised early, prior to expiry.
These options are contrasted with European options for which exercise is only permitted at expiry. Most traded stock and futures options are ‘American style’, while most index options are European.
The exercise style of listed options is American by default. Except for options on equity market indexes such as the S&P 500 index.
Options on futures are typically American as well.
The Black-Scholes pricing formulas are not applicable to American option pricing.
Being an algorithm, binomial option pricing models, nevertheless, can be modified to take care of the added complication in the American option.
Let’s see the differences between these two styles: European vs American options
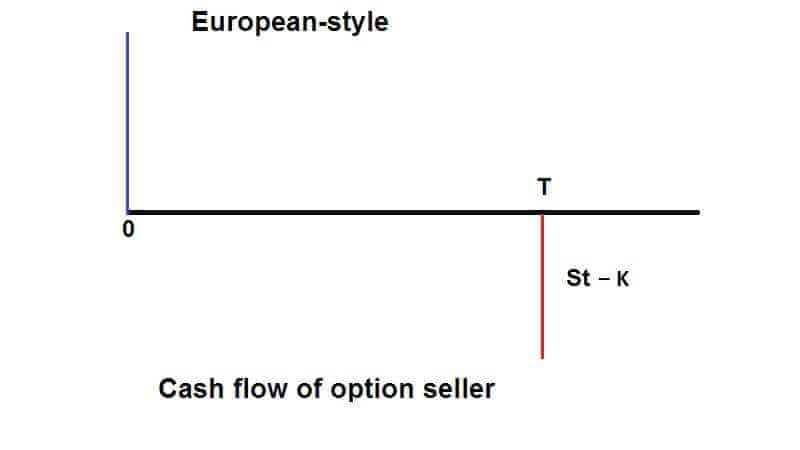
European-style
The seller sells the (call) option to allow the buyer to buy the underlying at the price of K on the expiration date only.
American-style
The seller sells the (call) option to allow the buyer to buy the underlying at the price of K and another option to buy at any time no later than the expiration date.
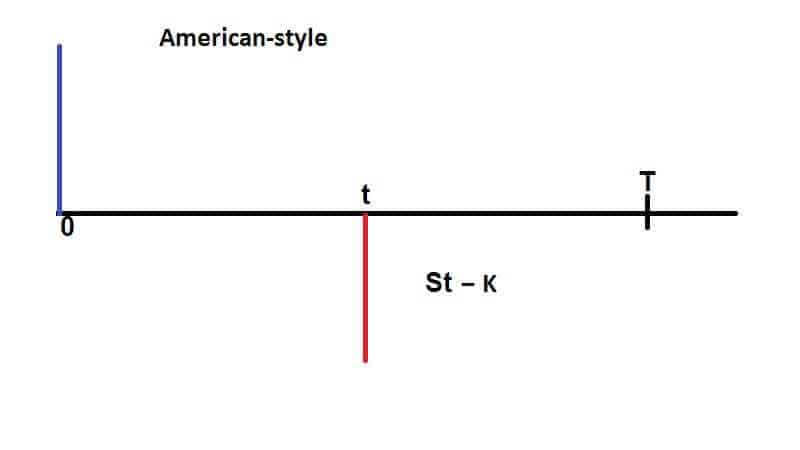
In these graphs, you can see the main difference.
The key difference between American and European options relates to when the options can be exercised: A European option may be exercised only at the expiration date of the option, i.e. at a single pre-defined point in time. An American option, on the other hand, may be exercised at any time before the expiration date.
American options can be exercised early
Unlike a European option, the holder of an American option can exercise the option before the expiry date. Because of this additional benefit, an American option is always more expensive than a European option.
However, is this benefit of any real use? Is there a situation where the option holder will get a better payoff by exercising the option early?
The answer is NO.
You should never early exercise an American option, especially if it’s a non-dividend paying stock. Let’s look at the reasoning behind this.
The option has intrinsic value and time value. The intrinsic value of the option is always greater than 0.
Along with that, the cash has time value. So, you would rather delay paying the strike price by exercising it. As late as possible.
You could use that money to earn interest.
So, a positive intrinsic value plus time value implies that you are better off selling the option rather than exercising it early. This is true for a non-dividend paying stock.
However, for a dividend paying stock, the only time it may pay to exercise a call option is the day before the stock goes ex-dividend. And only if the dividend minus the cost of carry is less than the corresponding Put.
By exercising, the option holder may forego the time value.
But don’t worry, it will make up from the dividend received.
We use the word ‘may’ because the dividend may not be high enough to justify the early exercise.
Here is the model for American options pricing. Here we take into account a put as an example.
Let
V = V (S, t)
be the option value.
At expiry, we still have
V (S, T)=(X − S) +
The early exercise feature gives the constraint
V (S, t) ≥ X − S
As before, we construct a portfolio of one long American option position and a short position in some quantity ∆, of the underlying.
Π = V − ∆S
With the choice ∆ = ∂V/∂S, the value of this portfolio changes by the amount
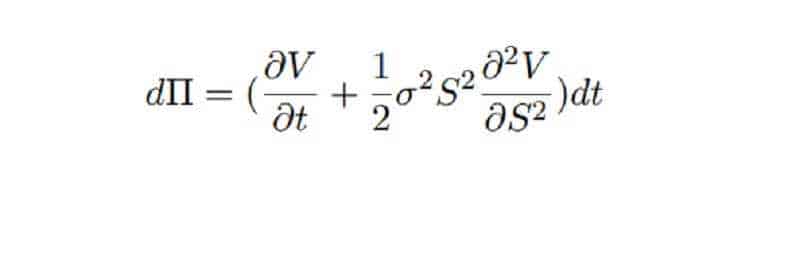
The advantage of the American style
The principal advantage of the American style of an option contract is the flexibility it offers to its holder as it can be exercised anytime before the expiration date T. Majority derivative contracts traded in financial markets are of the American style. In mathematical modeling of American options, unlike European style options, there is the possibility of early exercising the contract at some time t* ∈ [0, T) prior to the maturity time T.
It is well-known that pricing an American call option on an underlying stock paying continuous dividend yield q > 0 leads to a free boundary problem. In addition to a function V (t, S), we need to find the early exercise boundary function Sf (t), t ∈ [0, T].
The function Sf (t) has the following properties:
If Sf (t) > S for t ∈ [0, T] then V (t, S) > (S − E)+
If Sf (t) ≤ S for t ∈ [0, T] then V (t, S) = (S − E)+
The free boundary problem for pricing an American call option consists in finding a function V (t, S) and the early exercise boundary function Sf such that V solves the Black-Scholes PDE on a time depending domain:
{(t, S), 0 < S < Sf (t)} and V (t, Sf (t)) = Sf (t) − E, and ∂SV (t, Sf (t)) = 1
In a stylized financial market, the price of a European style option can be computed from a solution to the well-known Black–Scholes linear parabolic equation derived by Black and Scholes.
Recall that a European call option gives its owner the right but not the obligation to purchase an underlying asset at the expiration price E at the expiration time T.
But, let’s make American option pricing simpler
The value and pricing of stocks are fairly simple for most investors to understand. Basically, the value of a stock at any given time should reflect all known information about the company and the market.
However, increased volatility in option value occurs when the expiration date draws close or when it is already “in-the-money.” A call option is “in-the-money” when the present price of the underlying stock is higher than the strike price. A put option is considered to be “in-the-money” when the market price is lower than the strike price. When options are “in-the-money” or close to their expiration date, their value will change at a different rate than the underlying stock. However, the Black Scholes formula is a mathematical equation that can be used to approximate the value of an option relative to its market price.
Delta (Δ) in the Black Scholes formula is equal to the amount that the value of the option is expected to move for every 1 point of movement in the price of the underlying stock. Thus, if delta is 0.5 for stock A, then the value of the option for that stock will increase or decrease by 0.5 for every 1 point of fluctuation in the stock price.
In addition to being affected by proximity to the expiration date and being “in” or “out” of the money, the value of delta may change due to the overall volatility of the underlying stock itself.
There are times, however, when the Black Scholes formula fails to predict the value of the option.
The bottom line
The overall value of an option is actually determined by six factors: strike price, the current market price of an underlying stock, dividend yield, prime interest rate, proximity to the expiration date, and the volatility of the stock prices over the course of the option.
Because these six variables combine in different ways to affect the value of an option, it is possible for the price of the underlying stock to increase while the value of the option falls. The Black Scholes formula may fail when other factors are affecting the value of the option more than the current stock price.
American option pricing uses a “discrete-time” model of the varying price over time of the underlying financial instrument.


Leave a Reply